Quan hệ nhà đầu tư

Portfolio Blog: Tối ưu hóa danh mục đầu tư bằng Mean-Variance Analysis Markowitz

Bất cứ ai học đại học, dù chuyên ngành finance hay economics cũng đều nghe qua 1 bài toán về tối ưu hóa danh mục đầu tư. Đầu tiên là tính toán các thông số thống kê như mean, variance, correlation, sau đó tính toán trong excel chạy portfolio bao gồm 2 tài sản risky và 1 tài sản risk-free rate. Tuy nhiên, khi áp dụng vào thực tế, mọi chuyện trở nên khó hơn rất nhiều khi portfolio có nhiều hơn 2 tài sản (10 hoặc 100 hoặc 1000). Nếu hỏi bất kì sinh viên bachelor hay master nào về finance có lẽ cũng sẽ chém ầm ầm về capital market line, security market line hay CAPM. Tuy nhiên để code lại dc methodology từ các paper cũng như perform 1 cái optimization 1 cách thủ công thì có lẽ rất nhiều người bó tay. Và cuối cùng là cái gọi là modern portoflio theory này đúng hay sai trong thực tế thì cũng không ai trả lời 1 cách chính xác dc. Chỉ cần nhìn vào lượng citation của paper Markowitz (khoảng 20k), nếu chỉ chú ý đến phần critical review thì có rất nhiều thứ cần để quan tâm nếu muốn mang modern portfolio theory từ lý thuyết ra làm asset allocation ngoài thực tiễn. Vấn đề này nảy sinh trong lúc tôi đang học phần portfolio management của CFA, đặc biệt là sau khi tham dự 1 buổi lecture của 1 asset allocator 1 quỹ đầu tư bên Singapore. Có rất nhiều người giỏi trên thị trường, bằng cách này hay cách khác, tuy nhiên, cá nhân tôi thích những portfolio manager có cách tiếp cận xây dựng 1 portfolio một cách định lượng đầy tính khoa học. Ví dụ, khi research analyst đưa ra 1 con số từ định lượng như market share, profit, margin quý tới đến định tính như hành xử của đám đông, tin tức trên báo chí… portfolio manager phải bằng cách này hay cách khác đưa được các con số vào mô hình, thực hiện các tối ưu nó để đưa ra weight cụ thể cho từng asset classes (stock, bonds, FX….) hay hẹp hơn là securities selection (sectors, value, growth ….) thỏa mãn các ràng buộc tối thiếu investment horizon hay liquidity constraints. Hơn nữa phải đảm bảo portfolio phải có return ổn với dữ liệu historical data cũng như các tiêu chí đánh giá hiệu quả như sharpe ratio, treynor ratio, jensen ratio. Có rất nhiều vấn đề nảy sinh khi xây dựng 1 portfolio như vậy, và tôi sẽ lần lượt đề cập trong phần phía dưới cũng như các bài viết tiếp theo. 

Ở chuỗi bài viết blog này, tôi sẽ dùng R, Python hoặc Matlab để code lại 1 số findings của các key paper. R packages cũng có nhiều function có sẵn, tuy nhiên tôi sẽ nhìn sâu hơn vào source code cũng như so sánh sự khác biết trong kết quả giữa các function. Cần lưu ý là do R và Python là mã nguồn mở nên sẽ dễ cross-check hơn so với Matlab. Tôi sẽ dùng cả tiếng anh và tiếng việt vì giải thích các keyword bằng tiếng anh dễ hơn rất nhiều!!!

Đầu tiên là tổng quát về Modern Portfolio Theory (MPT). Cái này bắt nguồn từ công trình của 1 ông tên là Harry Markowitz. Vào năm 1952, ở tuổi 25, ông viết 1 bài báo nghiên cứu khoa học có tên là “Portfolio Selection” trên tạp chí Journal of Finance và đã đặt nền móng đầu tiên cho lý thuyết trên. Portfolio Theory của Markowitz giải thích cách chọn danh mục đầu tư dựa trên 3 thông số: Mean, Varriance, và Covariance của return của các tài sản riêng lẻ. Từ lý thuyết, các portfolio manager hay các asset-allocator sẽ sử dụng model trên để tính toán xác định phân bổ nguồn vốn vào các loại tài sản khác nhau.

Framework sơ khai nhất của MPT được gọi là Mean-Variance Analysis. Expected return của portfolio sẽ được tính toán cùng với risk tương ứng là variance/standard deviation và sự tương quan giữa các asset là covariance (correlation). Cũng từ đây khái niệm portfolio diversification ( đa dạng hóa danh mục đầu tư) được định nghĩa. Các định nghĩa khái niệm phía trên có thể dễ dàng tìm qua google hay textbook. MVA dựa trên 1 số giả định, giả định quan trọng nhất là investor sẽ đưa ra các quyết định đầu tư và dựa vào duy nhất 2 thông số của portfolio: risk và return. Ở đây risk được hiểu là standard deviation hay variance, thước đo cho cái gọi là uncertainty trong khi return có thể là arithmetic return hay geometric return tùy vào cách định nghĩa của mọi người. Sở dĩ việc lựa chọn standard deviation/variance là đơn vị đo lường cho risk cũng tạo nên những tranh luận không ngừng nghỉ trong giới học thuật cũng như các practitioners. Lý do quan trọng là khi sự uncertainty liên quan đến việc tăng giá của chứng khoán thì mọi người đều không bận tâm, vì tăng càng nhiều càng tốt. Người ta chỉ quan tâm đến việc giá chứng khoán giảm có nhiều không, giảm có liên tục không. Standard deviation hay variance thì lại tính cả 2 chiều tăng và giảm của giá, nên nhiều khi giá cổ phiếu tăng đều và đẹp cũng bị rơi vào diện có uncertainty cao. Đặc biệt là khi rất nhiều thị trường không cho phép short-sale hoặc short-sale 1 cách rất hạn chế với những mã thanh khoản thấp.

Vấn đề tối ưu hóa (optimization) sẽ được trình bày ngắn gọn qua 2 tình huống:

Ở một mức return kì vọng nhất định, investor sẽ chọn portfolio có lượng risk thấp nhất:

Với dạng ma trận trên, ta có hàm cần tối ưu hóa ở dạng bậc 2 (quadratic) với các ràng buộc ở dạng tuyến tính bậc 1 (linear).

Vấn đề có thể hiểu bằng cách ngược lại, tức là investor sẽ chọn portfolio với mức return cao nhất với 1 lượng rủi ro cho trước:

hàm cần tối ưu hóa ở dạng bậc 1 (linear) trong khi  ràng buộc có tồn tại ở cả dạng bậc 1 và bậc 2 (quadratic).

Lưu ý thêm là kí hiệu sigma ở trên đại diện cho covarriance matrix chứ không phải là sigma được dùng để tính tổng (hầu hết các textbook về MPT sử dụng ký hiệu sigma cho covarriance matrix trong bài toán trên).

Ở cả 2 cách tiếp cận trên, có thể thêm vào các ràng buộc khác như không có short-sale (weight của từng asset phải > hoặc =  0), weight không nhỏ hơn hay lớn hơn 1 giá trị cụ thể tùy vào điều kiện cụ thể.

Để cho dễ hình dung, hãy nhìn vào opportunity curve bên dưới:

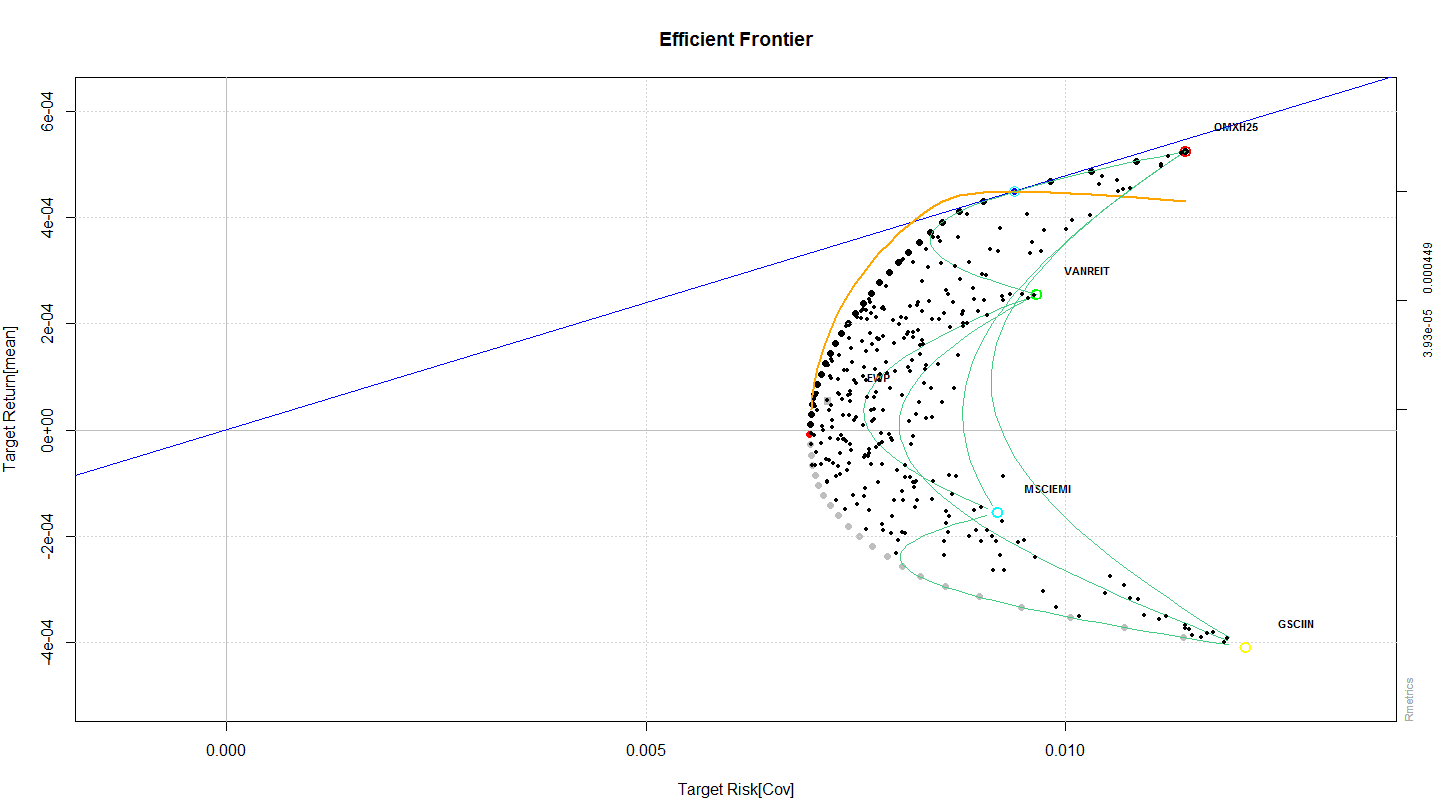
Giả sử tôi có 4 tài sản là OMX25, VANREIT, MSCIEMI và GSCIIN. Mỗi tài sản riêng lẻ sẽ có mean return, standard deviation và từng cặp correlation tương ứng. Khi kết hết chúng lại sẽ tạo ra các portofio có mean return và standard deviation khác nhau. vấn đề tối ưu hóa đề cập bên trên giống như tìm điểm có giá trị y cao nhất với 1 giá trị x nhất định (maximize return) hay tìm điểm có giá trị x nhỏ nhất với 1 giá trị y nhất định (minimize risk). Có 2 vấn đề nhỏ hơn:

• tìm điểm trên opportunity curve sao cho standard deviation/variance nhỏ nhất, được gọi là global-minimum variance problem. Điểm này là điểm cận trái của opportunity curve
• tìm điểm trên opportunity curve sao cho tỉ số mean return/ standard deviation hay (mean return – r0)/standard deviation là lớn nhất, được gọi là tangency portfolio problem.

Trong môi trường R có 1 hàm có thể phục vụ mục đích tối ưu hóa portfolio, đó là Solve.QP. Hàm Solve.QP sẽ giải quyết vấn đề tối ưu hóa theo phương pháp dual của Goldfard và Idanani (1982,1983) cho vấn đề hàm bậc 2 (quadratic programming problem):

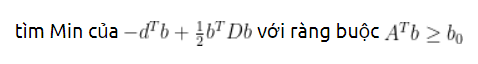
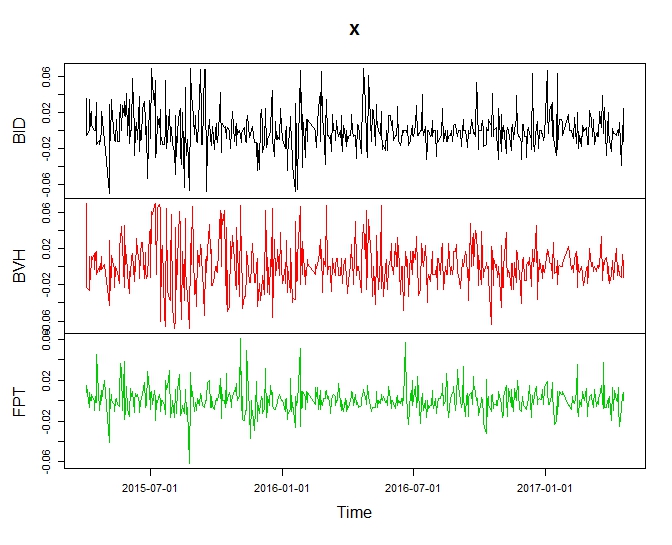
Trước khi đi vào phần tối ưu hóa, tôi sẽ lấy 3 mã cổ phiếu thuộc VN30 để phân tích: BID, BVH và FPT với dữ liệu daily return 2 năm từ 4/2015 tới 4/2017. Sẽ không có short-sale khi thực hiện tối ưu hóa.

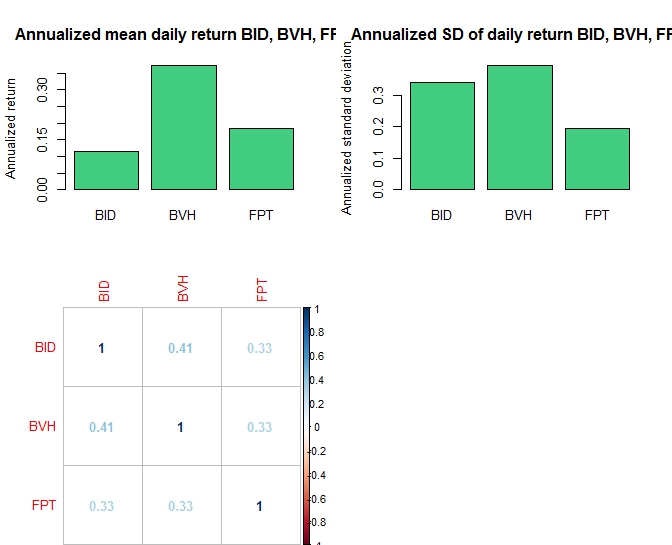
Với dữ liệu tính toán trên, tôi sẽ thực hiện mean-variance analysis với function solve.QP trong R để tính global mean-variance portfolio như bên dưới 

Tôi có vector weight của BID, BVH và FPT tương ứng là 13%, 5% và 82%. Test lại function trên bằng built-in function của Portfolio cho kết quả tương đương.  Source code của function minimumvariancePortfolio của package Portfolio cũng dùng hàm Solve.QP (check trên github) 

Tôi sẽ thử tính global mean variance analysis cho cả 30 mã trong rỏ VN30. Do HNG trong rỏ VN30 hiện tại không đủ data nên được tạm loại ra. 

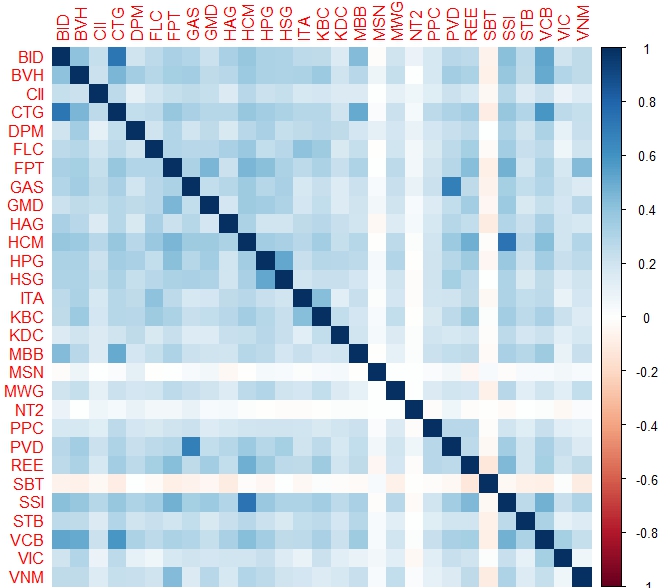
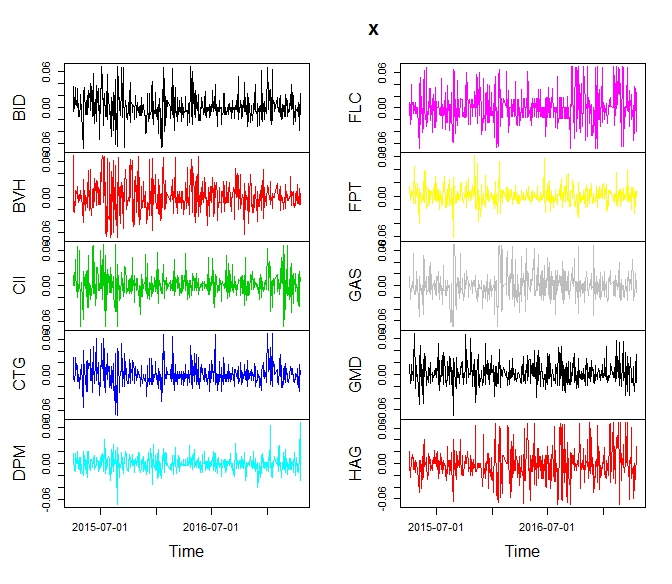
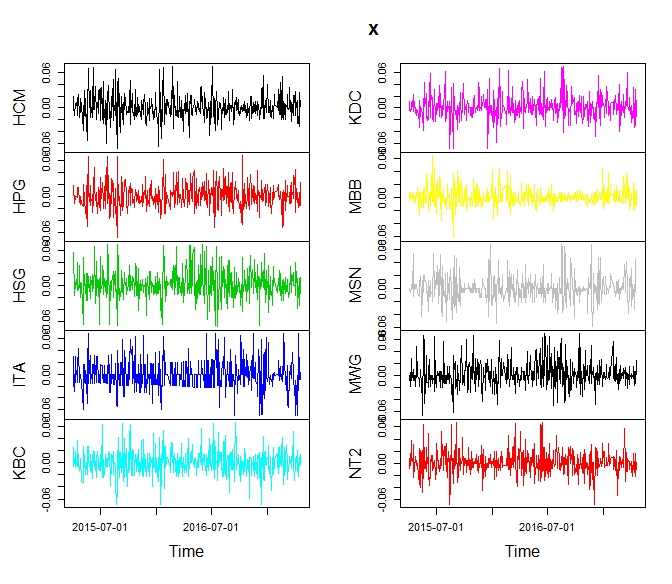
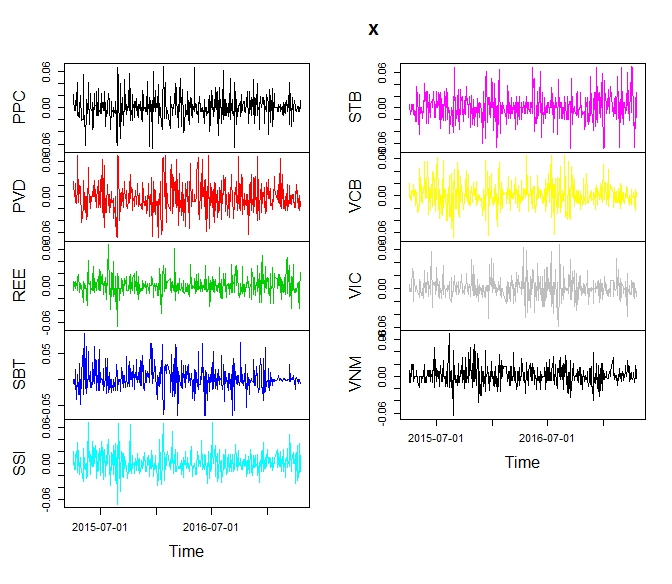
Nếu nhìn kĩ vào đồ thị daily return, chắc chắn có ít nhiều lợi ích diversification vì rất nhiều ngày có những mã trần sàn trong khi những mã khác giao động ở ngưỡng nhỏ hơn và ngược chiều nhau rất nhiều.

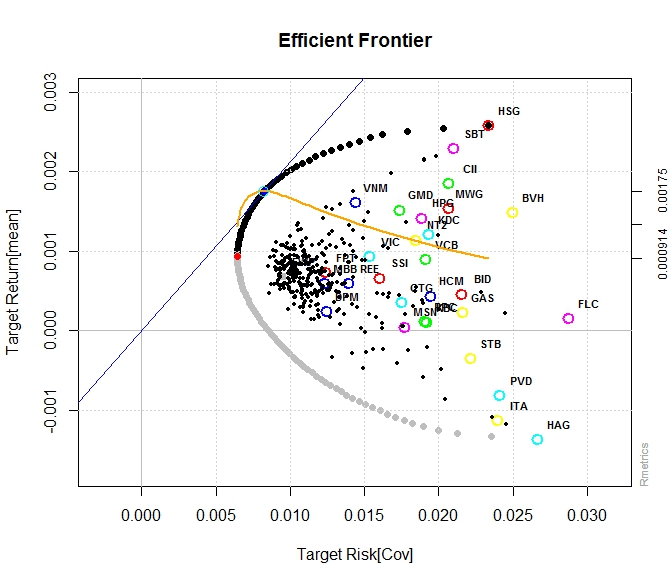
3 input quan trọng của mean variance analysis là mean, standard deviation/variance và covariance matrix. Ở phía bên trên tôi thực hiện optimization chủ yếu dựa vào historical data để tính ra weight của từng tài sản. Tuy nhiên trong thực tiễn, mean-variance analysis lấy số từ forecast của analyst để predict weight cho portfolio trong kì tới bởi nếu dùng historical data mà backtest fail hoặc bị overfitting thì phần lớn sẽ không tạo ra lợi nhuận. Hơn nữa chưa có các ràng buộc đến từng weight cho các tài sản liên quan đến volume trade, sector, maximum hay minimum weight trong phần optimization trên

p/s: Có lẽ bài viết phần nào bù đắp được phần kiến thức ở giữa lý thuyết trong các giáo trình tài chính định lượng và phần thực hành các phương pháp bằng các data thực tế. Quá trình đi từ lý thuyết sang thực tiễn đòi hỏi khả năng sử dụng phần mềm và coding ở tùy mức độ ( có 1 ví dụ tương đương trong kinh tế lượng, đó là việc sử dụng các toán tử ma trận để giải các bài toàn liên quan đến OLS, GLS … sau đó code lại trên ngôn ngữ máy, đóng gói thành các phần mềm với GUI và bán lại cho bên thứ 3 như các trường đại học hay tổ chức nghiên cứu). Để làm định lượng cho portfolio selection hay asset allocation, ở một mức vừa phải thì excel cũng khá đủ, ngay cả black-litterman cũng có thể code được bằng visual basic trong excel. Tuy nhiên, sử dụng R hay Python với các libraries có mã nguồn mở cũng có cái hay riêng của nó, đặc biệt là khi bạn được sử dụng các IDE đẹp đẽ hơn, syntax thông minh hơn và quá trình hỗ trợ từ các open-source từ developer cũng dễ dàng hơn. Ở phần 2 của blog tôi sẽ mô phỏng 1 tangency portfolio.

Reference: https://www.cfainstitute.org/learning/tools/topics/Pages/index.aspx

Nguồn: Ntlresearch